Parallel programming with Fortran 2008 and 2018 coarrays

Anton Shterenlikht
Mech Eng Dept, The University of Bristol, Bristol BS8 1TR, UK
mexas@bris.ac.uk

ABSTRACT

Coarrays were first introduced in Fortran 2008 standard. Coarrays are intended for single program - multiple data (SPMD) type parallel programming. Coarray features were significantly extended in Fortran 2018 standard. The runtime environment starts a number of identical executables (images) of the coarray program. Multiple physical processor cores or threads could be used. Each image has a unique number and a private address space. Ordinary variables are private to an image. Coarray variables are available for read/write access from any image. In HPC literature coarrays are often considered to be an example of partitioned global address space (PGAS) parallel programming model. Coarray communications are of "single side" type, i.e. a remote call from image A to image B does not need to be accompanied by a corresponding call in image B. This feature makes coarray programming a lot simpler than MPI. The standard provides synchronisation intrinsics to help avoid race conditions or deadlocks. In fact, a standard-confoming program should never deadlock or suffer races. Any ordinary variable can be made into a coarray - scalars, arrays, intrinsic or derived data types, pointers, allocatables - are all allowed. Coarrays can be declared in, and passed to, procedures. Coarrays are thus very flexible and can be used for a number of purposes. For example a collection of coarrays from all or some images can be thought of as a large single array. This is the opposite of the model partitioning logic, typical in MPI programs. A coarray program can exploit functional parallelism too, by delegating distinct tasks to separate images or teams of images. Coarray collectives, events, teams and facilities for dealing with failed images are defined in Technical Specification TS 18508 "Additional Parallel Features in Fortran", which will become a part of Fortran 2015 standard. Inter image communication patterns and data transfer are illustrated. A major unresolved problem of coarray programming is the lack of standard parallel I/O facility in Fortran. The course includes multiple code fragments and programming exercises with full solutions. Comparison is made with alternative parallel technologies - OpenMP, MPI and Fortran 2008 intrinsic DO CONCURRENT.

1. Coarray images

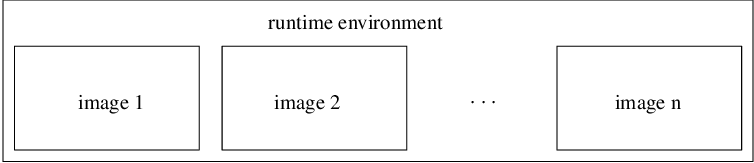
The runtime environment spawns a number of identical copies of the executable, called images. Hence coarray programs follow SPMD model.

$ cat one.f90
use iso_fortran_env, only: output_unit
implicit none
 integer :: img, nimgs
   img = this_image()
 nimgs = num_images()
 write (output_unit,"(2(a,i2))") "image: ", img, " of ", nimgs
end
$
$ ifort -o one.x -coarray -coarray-num-images=5 one.f90
$ ./one.x
image:  1 of  5
image:  3 of  5
image:  4 of  5
image:  2 of  5
image:  5 of  5
$

iso_fortran_env is the intrinsic module, introduced in Fortran 2003, and expanded in Fortran 2008. The module provides several named constants, such as input_unit, output_unit and error_unit, and several derived types.

All I/O units, except input_unit, are private to an image. However the runtime environment typically merges output_unit and error_unit streams from all images into a single stream. input_unit is preconnected only on image 1.

this_image and num_images are new intrinsics in Fortran 2008. this_image() with no arguments returns the index of the invoking image, starting from 1. num_images(), used always without arguments, returns the total number of images.

With Intel compiler one can set the number of images with the environment variable:

$ FOR_COARRAY_NUM_IMAGES=3
$ export FOR_COARRAY_NUM_IMAGES
$ ./one.x
image:  1 of  3
image:  2 of  3
image:  3 of  3
$

Note: as with MPI the order of output statements is unpredictable.

2. BlueCrystal

For details of the BlueCrystal consult

https://www.acrc.bris.ac.uk.

Use phase 3:

ssh bluecrystalp3.bris.ac.uk

Fortran coarrays on BlueCrystal can be used with either Intel Fortran or GCC/OpenCoarrays. To use Intel Fortran load the module with the latest ifort version:

module add languages/intel-compiler-16-u2

Several examples can be also run with the OpenCoarrays/GCC compiler:

http://opencoarrays.org

However, there is no module for it yet on phase 3.

The course materials are available from SourceForge:

https://sourceforge.net/projects/coarrays

You can either download the latest distribution, or pull the latest sources via subversion. To use subversion, you need to load this module:

module add tools/subversion-1.8.4

Make a directory for the course, and put the course materials there, e.g. with subversion:

mkdir zzz
cd zzz
svn co svn://svn.code.sf.net/p/coarrays/svn/head/ .

The example problems and the solutions are under examples.

Most Makefiles contain instructions to build executables both with the Intel compiler, ifort, and with GCC/OpenCoarrays, caf. If only one compiler is available, run make with -i, to ignore errors, as:

make -i

Many Makefiles also provide target run, to run the executables. Again, to ignore errors, e.g. due to build errors, try

make run -i

This document can be built with

make -C doc

The latest version of this document, in PDF and html formats, should be available at

http://coarrays.sourceforge.net

3. Example program: printing image number

cd examples/1img
make -i
make run -i

Tasks:

"Note that when a setting is specified in environment variable FOR_COARRAY_NUM_IMAGES, it overrides the compiler option setting."

4. Coarray syntax

The standard (ISO/IEC 1539-1:2010, 2010) uses the square brackets [], to denotes a coarray variable. A coarray variable can be also declared with codimension attribute. Any image has read/write access to all coarray variables on all images. It makes no sense to declare coarray parameters.

The last upper cobound is always an *, meaning that it is only determined at run time.

Examples of coarray variables:

integer :: i[*]                 ! scalar integer coarray with a single
                                ! codimension
integer, codimension(*) :: i    ! equivalent to the above


!                 lower  upper
!               cobound  cobound
!                     |  |
!                     |  |
!               upper |  |
!               bound |  |
!          lower |    |  |
!          bound |    |  |
!              | |    |  |
complex :: c(7,0:13) [-3:2,5,*] ! complex array coarray of corank 3
!            |  |       |  | |
!      subscripts       cosubscripts
!

Similar to ordinary Fortran arrays, corank is the number of cosubscripts. Each cosubscript runs from its lower cobound to its upper cobound. New intrinsics are introduced to return these values: lcobound and ucobound.

5. Cosubscript sets

this_image can take a coarray variable as an argument. In this case it returns a set of cosubscripts corresponding to the invoking image. New intrinsic image_index is the inverse of this_image. Given a valid set of cosubscripts as an input, image_index returns the index of the invoking image. Note that there can be subscript sets which do not map to a valid image index. For such invalid cosubscript sets image_index returns 0.

% cat cob.f90
program cob
implicit none
character( len=10 ) :: i[-2:2,2,1:*]
 if ( this_image() .eq. num_images() ) then
    write (*,*) "this_image()", this_image()
    write (*,*) "this_image( i )", this_image( i )
    write (*,*) "lcobound( i )", lcobound( i )
    write (*,*) "ucobound( i )", ucobound( i )
    write (*,*) "image_index(ucobound(i))", image_index( i, ucobound( i ) )
 end if
end program cob
% ifort -o cob.x -coarray cob.f90
% setenv FOR_COARRAY_NUM_IMAGES 20
% ./cob.x
 this_image()          20
 this_image( i )           2           2           2
 lcobound( i )          -2           1           1
 ucobound( i )           2           2           2
 image_index(ucobound(i))          20
% setenv FOR_COARRAY_NUM_IMAGES 24
% ./cob.x
 this_image()          24
 this_image( i )           1           1           3
 lcobound( i )          -2           1           1
 ucobound( i )           2           2           3
 image_index(ucobound(i))           0
%

6. Example program: cobounds and cosubscript sets

cd examples/2cob
make -i
make run -i

Tasks:

7. Remote operations, execution segments and image controlstatements

Remote operations are easily expressed in coarray notation. If a coarray variable does not have the square brackets, [], then the reference is to the variable of the invoking image. The syntax thus clearly indicates which statements involve remote operations.

integer :: i[*], j
real :: r(3,8) [4,*]
!
i[5] = i              ! remote write
r(:,:) = r(:,:) [3,3] ! remote read
i = j                 ! both i and j taken from the invoking image

There are several rules governing remote calls. Only one image can be referenced in each statement. For array coarrays the bracket notation, (), must be used. A valid set of cosubscripts must be used to refer to an image, not the image index.

A Coarray program consists of one or more execution segments. The segments are separated by image control statements. If there are no image control statements in a program, then this program has a single execution segment. sync all is a simple image control statement. If it is used on any image, then every image must execute this statement. On reaching this statement each image waits for each other. Its effect is in ordering the execution segments on all images. All statements on all images before sync all must complete before any image starts executing statements after sync all. In other words all images synchronise with each other. Thus sync all is a global barrier, similar to MPI routine MPI_Barrier.

integer :: i[*]              ! Segment 1 start
if (this_image() .eq. 1 ) &  ! Image 1 sets its value for i.
  i = 100                    ! Segment 1 end
                             !
                             ! All images must wait for image 1 to set its i,
                             ! before reading i from image 1.
sync all                     ! Image control statement
i = i[1]                     ! Segment 2 start - all images read i from image 1
end                          ! Segment 2 end

Note that not using the image control statement in this example will result in a race condition - some images might try to read i from image 1 before image 1 finished setting its value. However, the standard does not allow this:

"if a variable is defined on an image in a segment, it shall not be referenced, defined or become undefined in a segment on another image unless the segments are ordered"

Thus a standard conforming coarray program should not suffer from races.

All coarray programs implicitly synchronise at start and at termination.

Another new image control statement is sync images. It provides a more flexible means for image control. sync images takes a list of image indices with which it must synchronise:

if ( this_image() .eq. 3 ) sync images( (/ 2, 4, 5 /) )

There must be corresponding sync images statements on the images referenced by sync images statement on image 3, e.g.:

if ( this_image() .eq. 2 ) sync images( 3 )
if ( this_image() .eq. 4 ) sync images( 3 )
if ( this_image() .eq. 5 ) sync images( 3 )

Asterisk, *, is an allowed input. The meaning is that an image must synchronise with all other images:

if ( this_image() .eq. 1 ) sync images( * )
if ( this_image() .ne. 1 ) sync images( 1 )

In this example all images must synchronise with image 1, but not with each other, as would have been the case with sync all.

For cases when there are multiple sync images statements with identical sets of image indices, the standard sets the rules which determine which sync images statements correspond:

"Executions of SYNC IMAGES statements on images M and T correspond if the number of times image M has executed a SYNC IMAGES statement with T in its image set is the same as the number of times image T has executed a SYNC IMAGES statement with M in its image set. The segments that executed before the SYNC IMAGES statement on either image precede the segments that execute after the corresponding SYNC IMAGES statement on the other image."

Here’s an example of swapping coarray values between two images.

$ cat swap.f90
integer :: img, nimgs, i[*], tmp
                                 ! implicit sync all
  img = this_image()
nimgs = num_images()
   i = img                       ! i is ready to use

 if ( img .eq. 1 ) then
   sync images( nimgs )          ! explicit sync 1 with last img
    tmp = i[ nimgs ]
   sync images( nimgs )          ! explicit sync 2 with last img
      i = tmp
 end if


 if ( img .eq. nimgs ) then
   sync images( 1 )              ! explicit sync 1 with img 1
    tmp = i[ 1 ]
   sync images( 1 )              ! explicit sync 2 with img 1
      i = tmp
 end if
 write (*,*) img, i
                                 ! all other images wait here
end
$ ifort -coarray swap.f90
$ setenv FOR_COARRAY_NUM_IMAGES 5
$ ./a.out
           3           3
           1           5
           2           2
           4           4
           5           1
$

How many execution segments are there on each image?

Which sync images statements correspond?

8. Example program: segments and image control statements

cd examples/3swap
make -i
make run -i

Tasks:

9. Example program: deadlock

cd examples/4deadlock
make -i
make run -i

Tasks:

10. New Fortran 2008 construct: DO CONCURRENT

This do loop is intended for cases when the order of loop iterations is of no importance. The idea is that such loops can be optimised by a compiler.

integer :: i, a1(100)=0, a2(100)=1
do concurrent( i=1, 100 )
  a1(i) = i                ! valid, independent
  a2(i) = sum( a2(1:i) )   ! invalid, order is important
end do

The exact list of restrictions on what can appear inside a do concurrent loop is long. These restrictions severely limit the usefulness of the do concurrent construct. While this new construct is potentially a portable parallelisation tool, there might or might not be a performance gain, depending on the implementation. In this tutorial do concurrent is used for comparison with coarrays in the 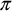calculation example.

11. Implementation and performance

The standard deliberately (and wisely) says nothing on this.

A variety of underlying parallel technologies can be, and some are, used - MPI, OpenMP, SHMEM, GASNet, ARMCI, DMAPP, etc. As always, performance depends on a multitude of factors.

The Standard expects, but does not require, that coarrays are implemented in a way that each image knows the address of all coarrays in memories of all images, something like the integer coarray i in the illustration below. This is sometimes called symmetric memory. An ordinary, non-coarray, variable r might be stored at different addresses by different processes. Cray compiler certainly does this, other compilers likely do too.

Example: calculation of using the Gregory - Leibniz series:

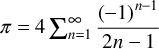
Given the series upper limit, each image sums the terms beginning with its image number and with a stride equal to the number of images. Then image 1 sums the contributions from all images. The segments are ordered by sync all to make sure all images finish calculating their partial sums before image 1 reads the values from all other images and adds those together.

Below is a sample scaling performance with ifort on 16-core nodes with 2.6Hz SandyBridge cores. As always, a great many things affect performance, coarrays are no exception.

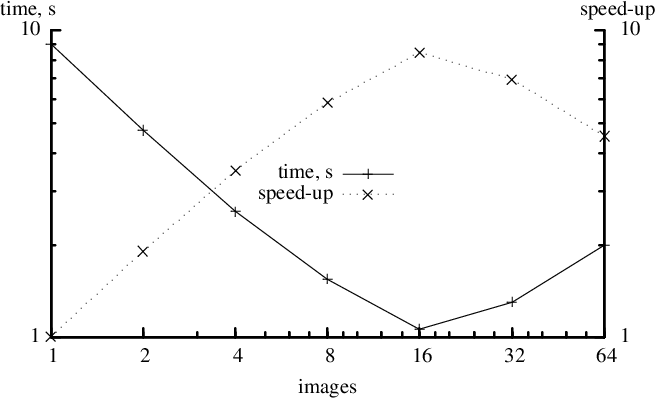
The key segment of the code, - the loop for partial 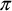, and the calculation of the total 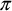value, is shown below for the coarray code, and also for MPI, Fortran 2008 new intrinsic DO CONCURRENT and OpenMP.

11.1. Coarrays

do i = this_image(), limit, num_images()
 pi = pi + (-1)**(i+1) / real( 2*i-1, kind=rk )
end do
 sync all              ! global barrier
if (img .eq. 1) then
  do i = 2, nimgs
    pi = pi + pi[i]
  end do
  pi = pi * 4.0_rk
end if

11.2. MPI

do i = rank+1, limit, nprocs
 pi = pi + (-1)**(i+1) / real( 2*i-1, kind=rk )
end do
call MPI_REDUCE( pi, picalc, 1, MPI_DOUBLE_PRECISION, &
                 MPI_SUM, 0, MPI_COMM_WORLD, ierr )

picalc = picalc * 4.0_rk

11.3. DO CONCURRENT

loops = limit / dc_limit
do j = 1, loops
  shift = (j-1)*dc_limit
  do concurrent (i = 1:dc_limit)
    pi(i) = (-1)**(shift+i+1) / real( 2*(shift+i)-1, kind=rk )
  end do
  pi_calc = pi_calc + sum(pi)
end do

pi_calc = pi_calc * 4.0_rk

11.4. OpenMP

!$OMP PARALLEL DO DEFAULT(NONE) PRIVATE(i) REDUCTION(+:pi)
do i = 1, limit
 pi = pi + (-1)**(i+1) / real( 2*i-1, kind=rk )
end do
!$OMP END PARALLEL DO

pi = pi * 4.0_rk

Coarray implementation is closest to MPI. When coarray collectives are in the standard, the similarity will be even greater.

The table below is a subjective comparison of these four parallelisation methods.

12. Example program: calculation of

cd examples/5pi
make -i
make run -i

For comparison, the same problem is solved with coarrays, do concurrent, OpenMP and MPI. The source code files are: (1) coarray - pi_ca.f90, (2) do concurrent - pi_dc.f90, (3) OpenMP - pi_omp.f90 and (4) MPI pi_mpi.f90.

Tasks

13. Another scaling example

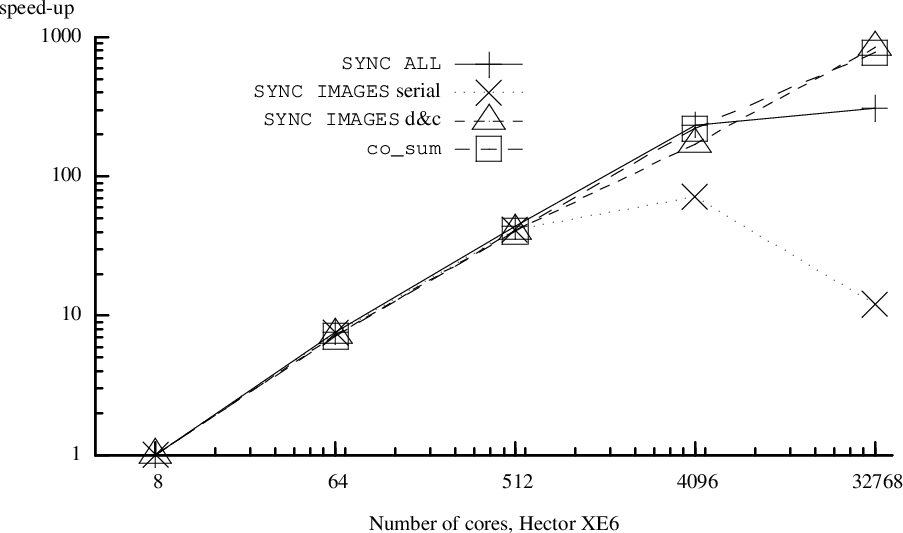
This scaling data was obtained on Hector, the previous generation UK national supercomputer. The code is a microstructure simulation cellular automata model (Shterenlikht, 2015; Shterenlikht, 2013). Three orders of magnitude speed-up has been achieved between 8 and 32k cores, an efficiency of about 25%.

co_sum is at present a Cray extension to the standard. This is a collective sum operation. Note that even sync all shows very impressive scaling, despite being the simplest image control statement, a global barrier.

14. Allocatable coarrays and coarray of derived types withallocatable components

Coarray variables can be allocatable. Allocatable coarrays are declared with : for each dimension and each codimension:

real, allocatable :: r(:) [:]      ! real allocatable array coarray
complex, allocatable :: c[:]       ! complex allocatable scalar coarray
integer, allocatable :: i[:,:,:]   ! integer allocatable scalar coarray
                                   ! with 3 codimensions

As with non-allocatable coarray, the last upper codimension must be an asterisk on allocation, to allow for the number of images to be determined at runtime:

allocate( r(100) [*], source=0.0 )
allocate( c[*], source=cmplx(0.0,0.0) )
allocate( i[7,8,*], source=0 )

Sourced allocation was added in Fortran 2003.

Allocation and deallocation of coarrays involve implicit image synchronisation. Hence coarray allocation/deallocation must appear only in contexts which allow image control statements. This means that all images must allocate and deallocate allocatable coarrays together. All allocated coarrays are automatically deallocated at program termination.

Coarrays must be allocated with the same bounds and cobounds on all images.

The following coarray allocations are not valid because the bounds or cobounds are not identical on all images. However, the processor (compiler) is not required to detect this violation of the standard.

allocate( r(10*this_image()) [*], source=0.0 )   ! not valid
allocate( i[7*this_image(), 8,*], source=0 )     ! not valid

Allocatable coarrays can be passed as arguments to subroutines. If a coarray is allocated in a subroutine, the dummy argument must be declared with intent( inout ). The bounds and cobounds of the actual argument must match those of the dummy argument.

module coalloc
 contains
 subroutine coal(i, b, cob)
   integer, allocatable, intent(inout) :: i(:) [:,:]
   integer, intent(in) :: b, cob
   allocate( i(b) [cob,*], source=0 )
 end subroutine coal
end module coalloc


program z
 use coalloc
 integer, allocatable :: i(:) [:,:]
 call coal( i, 8, 4 )
end program z

If remote access arrays with different bounds are needed on different images, a simple solution is to declare a coarray of a derived type with an allocatable component:

$ cat pointer.f90
program z
implicit none
  type t
    integer, allocatable :: i(:)
  end type
    type(t) :: value[*]
    integer :: img
 img = this_image()
 allocate( value%i(img), source=img )   ! not coarray - no sync
 sync all
 if ( img .eq. num_images() ) value%i(1) = value[ 1 ]%i(1)
 write (*,*) "img", img, value%i
end program z
$ ifort -coarray -warn all -o pointer.x pointer.f90
$ setenv FOR_COARRAY_NUM_IMAGES 3
$ ./pointer.x
 img           1           1
 img           2           2           2
 img           3           1           3           3
$

Note that gfortran 6 still does not support coarrays of derived type with allocatable components.

15. Example program: allocatable component of a derivedtype

cd examples/6pointer
make -i
make run -i

Tasks

16. Example program: allocatable coarray

cd examples/7alloc
make -i
make run -i

Tasks

17. Termination

In a coarray program a distinction is made between a normal and error termination.

Normal termination on one image allows other images to finish their work. STOP and END PROGRAM initiate normal termination.

New intrinsic ERROR STOP initiates error termination. The purpose of error termination is to terminate all images as soon as possible.

Example of a normal termination:

$ cat term.f90
implicit none
integer :: i[*], img
real :: r
img = this_image()
  i = img
if ( img-1 .eq. 0 ) stop "img cannot continue"
do i=1,100000000
 r = atan(real(i))
end do
write (*,*) "img", img, "r", r
end
$ ifort -coarray term.f90 -o term.x
$ ./term.x
img cannot continue
 img           2 r   1.570796
 img           4 r   1.570796
 img           3 r   1.570796
$

Image 1 has encountered some error condition and cannot proceed further. However, this does not affect other images. They can continue doing their work. Hence STOP is the best choice here.

Example of an error termination:

$ cat errterm.f90
implicit none
integer :: i[*], img
real :: r
img = this_image()
  i = img
if ( img-1 .eq. 0 ) error stop "img cannot continue"
do i=1,100000000
 r = atan(real(i))
end do
write (*,*) "img", img, "r", r
end
$ ifort -coarray errterm.f90 -o errterm.x
$ ./errterm.x
img cannot continue
application called MPI_Abort(comm=0x84000000, 3) - process 0
rank 0 in job 1  newblue3_53066   caused collective abort of all ranks
  exit status of rank 0: return code 3
$

Here the error condition on image 1 is severe. It does not make sense for other images to continue. ERROR STOP is the appropriate choice here.

Note: the following does not seem to be supported by the Intel compiler v.15.

The standard provides a way to determine, via image control statements sync images and sync all, whether any image has initiated normal termination. For this both statements can use stat= specifier. If at the point of an image control statement some image has already initiated normal termination, then the integer variable given to stat= will be defined with the constant stat_stopped_image from the intrinsic module iso_fortran_env. The images that are still executing might decide to take a certain action with this knowledge:

use, intrinsic :: iso_fortran_env
integer :: errstat=0
  ! all images do work
sync all( stat=errstat )
if ( errstat .eq. stat_stopped_image ) then
  ! save my data and exit
end if
! otherwise continue normally

Below is a schematic flowchart illustrating steps taken during normal and error termination.

18. Example program: normal and error termination

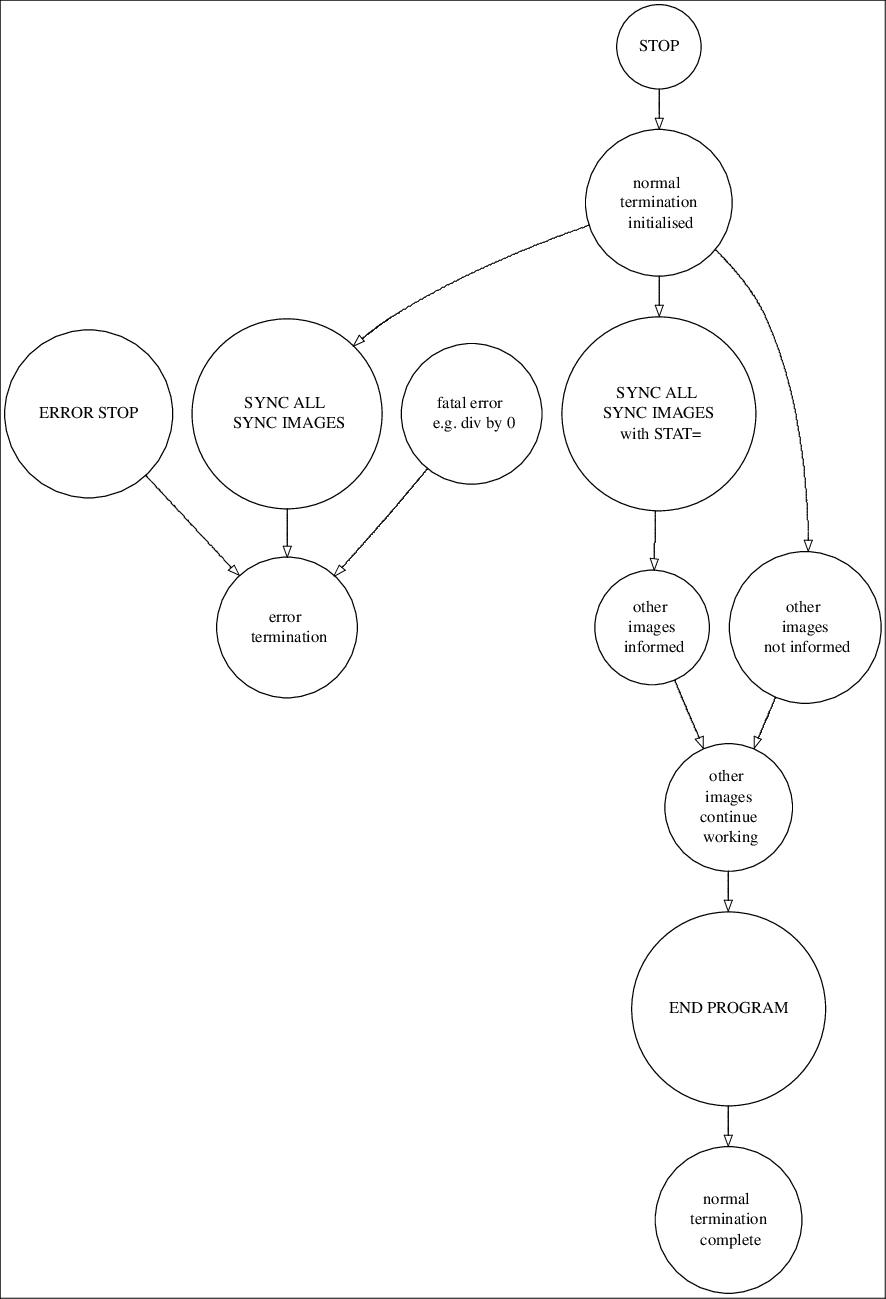
cd examples/8term
make -i
make run -i

Tasks

19. Example: parallel image processing

This example implements a halo exchange algorithm to speed up an image processing program. You will need to view images on screen, so connect to BlueCrystal with ssh -X or ssh -XY.

Go to the example files:

cd examples/9laplace

If using the Intel compiler use Makefile.ifort as

make -f Makefile.ifort

If using the OpenCoarrays/GCC compiler, use Makefile.oca as

make -f Makefile.oca

In either makefile there is a target run to run all executables one after another with some command line arguments, as:

make run

Make sure to check those arguments before running.

This directory contains several programs, each producing a separate output file.

File ref.pgm is the reference picture:

To avoid confusion with coarray images, we use "picture" in this example to refer to a graphical image. This is a photo of Cray XC30, similar to the one installed as Archer, the current UK national supercomputer. ref_edge.pgm is a reference edge file:

pgmio.f90 is a module dealing with reading and writing of the PGM files.

If the picture is read into a 2D array p, then the 2D array of edges, e, can be calculated like this:

e(i,j) = p(i-1,j) + p(i+1,j) + p(i,j-1) + p(i,j+1) - 4 * p(i,j)

where i takes values between lbound(p, dim=1) and ubound(p, dim=1) and j takes values between lbound(p, dim=2) and ubound(p, dim=2).

Note that the expression for e uses values outside of the actual data array. So we need to extend the array sizes by one in each direction to store the "halo" elements.

You might recognise that the expression for e is a Laplacian of the original picture intensity:

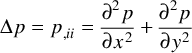
Given the edges of a picture, it is possible to reconstruct the original picture, i.e. solve the Laplace equation, e.g. using the iterative Jacobi method. Inverting the expression for e we get the following simple iterative algorithm:

pnew(i,j) = 0.25 * ( p(i-1,j) + p(i+1,j) + p(i,j-1) + p(i,j+1) - e(i,j) )
        p = pnew

which is repeated until convergence.

However, convergence of this algorithm is very slow. Typically 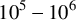iterations are required. We will use coarrays to speed-up the execution.

The key idea is to partition the picture into smaller fragments, and delegate processing of each fragment to a separate processor (image). The picture may be partitioned along dimension 1:

or along dimension 2:

or along both dimensions 1 and 2:

Tasks:

20. Next standard

The latest draft of the 2015 standard is:

http://j3-fortran.org/doc/meeting/210/16-007r1.pdf

The list of features included in the next revision of Fortran standard was finalised in 2015 in WG5 document N2082:

http://isotc.iso.org/livelink/livelink?func=ll&objId=17357018&objAction=Open

It will have new coarray features, detailed in the technical specification (TS18508, 2015):

http://isotc.iso.org/livelink/livelink?func=ll&objId=17288706&objAction=Open

TS 18508 includes:

21. Collectives

Collective intrinsics are added in Fortran 2018 (TS18508, 2015). These are already available in gfortran6.

CO_BROADCAST
CO_MIN
CO_MAX
CO_REDUCE
CO_SUM

It’s very useful to have the text of TS 18508 at hand for reference:

http://isotc.iso.org/livelink/livelink?func=ll&objId=17288706&objAction=Open

Note that the TS uses the term "all images in the current team". To date teams are available neither in ifort 16 nor in gfortran6. Hence, for simplicity, we say instead "all images", ignoring teams for now.

The five procedures have similar interfaces:

CO_MAX (A [, RESULT_IMAGE, STAT, ERRMSG])
CO_MIN (A [, RESULT_IMAGE, STAT, ERRMSG])
CO_SUM (A [, RESULT_IMAGE, STAT, ERRMSG])
CO_BROADCAST (A, SOURCE_IMAGE [, STAT, ERRMSG])
CO_REDUCE (A, OPERATOR [, RESULT_IMAGE, STAT, ERRMSG])

The arguments inside [] are optional.

For CO_MAX CO_MIN CO_SUM argument A must of a numeric kind. It must be of the same type and type parameters on all images. It can be an array, in which case it must have the same shape on all images. But A does not need to be a coarray! These 3 procedures will perform elemental max, min and sum operations respectively.

RESULT_IMAGE is an integer scalar. If this optional argument is present then the result of a collective operation will be assigned to A only on that image. A will be overwritten on that image only. RESULT_IMAGE is absent, then the result will be assigned to A on all images. A will be overwritten on all images. A will be overwritten

If a collective procedure was successful, STAT is set to zero. In case of an error condition during the execution of a collective procedure on any image, STAT will receive a non-zero value, and ERRMSG will be set to some explanatory messagy by the processor.

There are several special failure cases that can be distinguished. If a collective procedure fails because some image(s) initiated a normal termination, then STAT will be set to STAT_STOPPED_IMAGE on all images, which is defined in ISO_FORTRAN_ENV intrinsic module. Otherwise STAT will be zero. If some image(s) are detected to have failed, then STAT will be set to STAT_FAILED_IMAGE on all images. For other failure conditions processor will set STAT to a non-zero value which is different from either STAT_STOPPED_IMAGE or STAT_FAILED_IMAGE.

SOURCE_IMAGE is an integer scalar input argument indicating the image from where A will be broadcast to all images.

Finally, CO_REDUCE provides a general reduction facility over all images. OPERATOR is a pure function with 2 scalar arguments of the same type and type parameters. The value of A is calculated by CO_REDUCE iteratively. Values of A from all images are added to a set. Each iteration function OPERATOR is called for 2 arguments A from this set, taken from 2 images. The result is written to the set, and the 2 arguments are removed from the set. The iterative procedure continues until there is only a single element is left in the set. This is the result of this collective procedure.

22. Example program: collectives

cd examples/10collectives
make -i
make run -i

Try to use sort to separate screen output, e.g.

make run -i | sort -k3 -r

Tasks:

23. Coarray resources

The standard is the best reference. Draft version is available online:

http://j3-fortran.org/doc/year/10/10-007r1.pdf

Four further documents with correction to the standard (corrigenda) have been published since 2010 (N1903, 2012; N1958, 2013; N2003, 2014; N2095, 2016), which are also available online:

ftp://ftp.nag.co.uk/sc22wg5/N1901-N1950/N1903.pdf
ftp://ftp.nag.co.uk/sc22wg5/N1951-N2000/N1958.pdf
ftp://ftp.nag.co.uk/sc22wg5/N2001-N2050/N2003.pdf
http://isotc.iso.org/livelink/livelink?func=ll&objId=17532810&objAction=Open

All Fortran standard development documents are available from the official WG5 pages:

http://www.nag.co.uk/sc22wg5

A more readable resource, but just as thorough, is the "MFE" book (Metcalf, 2011).

Sections on coarrays, with examples, can be found in several further books (Brainerd, 2015; Chivers, 2015; Markus, 2012; Hanson, 2013; Clerman, 2012).

At this time Fortran 2008 coarrays are fully supported by the Cray and the Intel v.16 compilers. OpenCoarrays project, http://opencoarrays.org, provides a transport library for GCC starting from version 5.1 (Fanfarillo, 2014; Chivers, 2015). However, OpenCoarrays/GCC does not support all features of the Fortran 2008 standard. Notably, coarrays of derived type with allocatable or pointer components are not fully supported.

Cray and OpenCoarrays/GCC support selected collectives from TS 18508 (TS18508, 2015).

OpenUH (University of Houston) open source compiler, http://web.cs.uh.edu/~openuh, claims to fully support coarrays, but I haven’t tried it. The lastest distribution is from 2015.

The Rice coarray compiler, http://caf.rice.edu, doesn’t seem to be actively developed since 2011, although it is used in CS for compiler research purposes.

The Fortran mailing list, COMP-FORTRAN-90@JISCMAIL.AC.UK

https://www.jiscmail.ac.uk/cgi-bin/webadmin?A0=comp-fortran-90

and the Fortran Usenet newsgroup, comp.lang.fortran, are invaluable resources for all things Fortran, including coarrays.

24. Profiling coarray programs

This is advanced material for those who are mostly interested in performance of parallel programs. Directory

examples/prof

includes profiling examples. At present there are only examples for TAU, (Tuning and Analysis Utilities).

24.1. Profiling with TAU

TAU, (Tuning and Analysis Utilities):

https://www.cs.uoregon.edu/research/tau/home.php

is a very popular tool, or rather a collection of tool for instrumenting of parallel programs for profiling and/or tracing experiments. It can also collect multiple hardware counters via PAPI (Performance Application Programming Interface):

http://icl.cs.utk.edu/papi/

The TAU team are working on adding coarrays support to PDT (Program Database Toolkit):

https://www.cs.uoregon.edu/research/pdt/home.php

However, at present, PDT doesn’t understand coarray syntax yet, so TAU instrumentation is compiler based.

TAU is highly portable. TAU is actively developed and there is an extensive manual online. TAU examples are under

examples/prof/tau

Refer to README files for building and execution examples.

In these examples TAU 2.25.1 and PAPI 5.3.0 are used.

At present, a call to a TAU routine to set the node must be included:

call TAU_PROFILE_SET_NODE(this_image())

See

https://www.cs.uoregon.edu/research/tau/docs/newguide/rn01re86.html

for more details.

After an instrumented program was run, profiling data can be examined with a command line tool pprof, or with a GUI tool paraprof. An snippet from a pprof output can show something like this when using the Intel compiler:

NODE 10;CONTEXT 0;THREAD 0:
---------------------------------------------------------------------------------------
%Time    Exclusive    Inclusive        Call       Subrs  Inclusive Name
              msec   total msec                          usec/call
---------------------------------------------------------------------------------------
 35.9       21,261       21,261      180000           0        118 .TAU application => coback1tau => MPI_Recv()
 35.9       21,261       21,261      180000           0        118 MPI_Recv()
 33.6       19,880       19,880 1.65962E+06           0         12 MPI_Win_unlock()
 29.1       17,183       17,183      900093           0         19 .TAU application => coback1tau => MPI_Win_unlock()
 83.5        9,819       49,407           1 1.48008E+06   49407127 .TAU application => coback1tau
 83.5        9,819       49,407           1 1.48008E+06   49407127 coback1tau

This particular output was generated with pprof -m which sorts the data by the exclusive total time. One can learn from the above data that MPI_Recv and MPI_Win_unlock account for most of the run time. The program itself is coback1tau which is under

examples/prof/tau/9laplace

and it accounts for only about 10s, whereas the two above MPI routines account for over 40s. This clearly shows that the run time is heavily dominated by the MPI calls.

An example paraprof result can be seen below.

This is the same data as printed by pprof, just presented as a colour histogram. This particular output is for image 3, where MPI_Win_unlock dominates.

Tracing data can be visualised with Jumpshot-4:

http://www.mcs.anl.gov/research/projects/perfvis/software/viewers/

which is bundled with the TAU distribution.

A sample result is shown below.

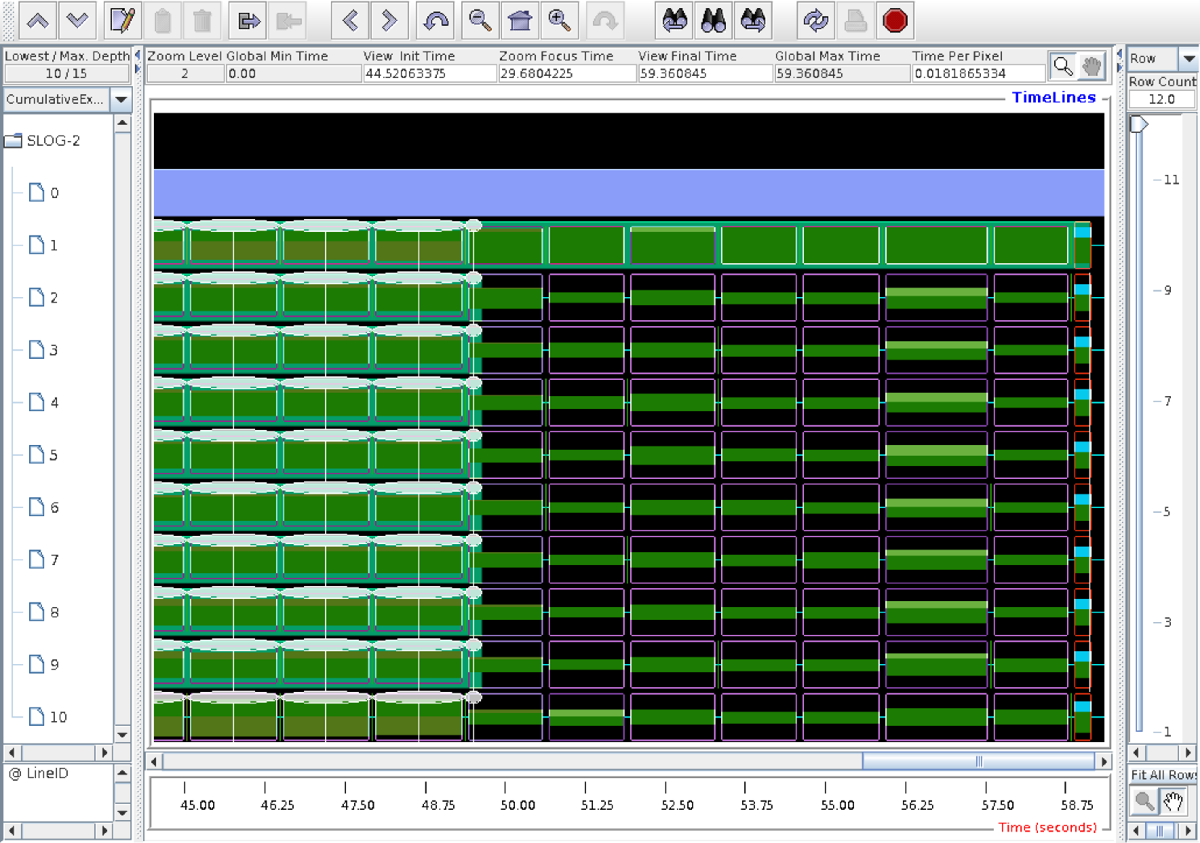
This is a fragment of a trace on 10 images. Note there is also image (node) 0 shown, which runs caflaunch process, shown in lavender colour. This is an Intel process, probably designed to launch the coarray environment.

More details on coarray profiling and tracing with TAU can be seen on CGPACK pages, e.g.:

http://cgpack.sourceforge.net/201605res/
http://cgpack.sourceforge.net/201604res/
http://cgpack.sourceforge.net/201603res/

See also (Radhakrishnan, 2015; Haveraaen, 2015).

References

W. S. Brainerd, Guide to Fortran 2008 programming, Springer (2015).

I. Chivers and J. Sleightholme, Introduction to Programming with Fortran, Springer, 3 Ed. (2015).

I. D. Chivers and J. Sleightholme, “Compiler support for the Fortran 2003 and 2008 standards,” ACM Fortran Forum 34, pp. 7-27, revision 17 (2015).

N. S. Clerman and W Spector, Modern Fortran: style and usage, Cambridge (2012).

A. Fanfarillo, T. Burnus, S. Filippone, V. Cardellini, D. Nagle, and D. Rouson, “OpenCoarrays: open-source transport layers supporting coarray Fortran compilers” in PGAS 2014, Eugene, Oregon, USA, Oct. 7-10 (2014). http://www.opencoarrays.org/uploads/6/9/7/4/69747895/pgas14_submission_7-2.pdf.

R. J. Hanson and T. Hopkins, Numerical Computing with Modern Fortran, SIAM (2013).

Haveraaen, M., Morris, K., Rouson, D., Radhakrishnan, H., and Carson, C., “High-Performance Design Patterns for Modern Fortran,” SCIENTIFIC PROGRAMMING, p. 942059 (2015). DOI: 10.1155/2015/942059.

ISO/IEC 1539-1:2010, Fortran - Part 1: Base language (2010).

A. Markus, Modern Fortran in practice, Cambridge (2012).

M. Metcalf, J. Reid, and M. Cohen, Modern Fortran explained, Oxford, 7 Ed. (2011).

N1903, “Fortran - Part 1: Base language TECHNICAL CORRIGENDUM 1,” ISO/IEC 1539-1:2010/Cor 1:2012 (2012).

N1958, “Fortran - Part 1: Base language TECHNICAL CORRIGENDUM 2,” ISO/IEC 1539-1:2010/Cor 2:2013 (2013).

N2003, “Fortran - Part 1: Base language TECHNICAL CORRIGENDUM 3,” ISO/IEC 1539-1:2010/Cor 3:2014 (2014).

N2095, Draft ISO/IEC 1539-1:2010 TECHNICAL CORRIGENDUM 4 (2016).

Radhakrishnan, H., Rouson, D. W. I., Morris, K., Shende, S., and Kassinos, S. C., “Using Coarrays to Parallelize Legacy Fortran Applications: Strategy and Case Study,” SCIENTIFIC PROGRAMMING, p. 904983 (2015). DOI: 10.1155/2015/904983.

A. Shterenlikht and L. Margetts, Proc. Roy. Soc. A 471, p. 20150039 (2015).

A. Shterenlikht in Proc. 7th PGAS Conf., The University of Edinburgh, UK (2013).

TS18508, “Additional Parallel Features in Fortran,” ISO/IEC JTC1/SC22/WG5 N2074 (2015).